Long-term holding risk
Leveraged and inverse products (L&I Products) seek to track a multiple of or a multiple of the opposite of the return of its underlying index on a daily basis and they are not intended for holding longer than one day. If a L&I Product is held for longer than one day, its cumulative return may not be equal to the multiple of or the multiple of the opposite of the cumulative return of the underlying index.
Such deviation effect becomes more pronounced (i) when the underlying index experiences volatility; (ii) for larger leverage factor; (iii) for inverse exposure; and/or (iv) for longer holding periods. Investors should not expect the actual percentage return of investing in the L&I Product to be equal to the multiple and/or the inverse multiple change in the underlying index for periods of longer than one day.
Examples
- Upwards trending market
In an upwards trending market where the underlying index rises by 4% and 6% on Day 1 and Day 2 respectively, the 2x leveraged product will make a gain of 8% and 12% on Day 1 and Day 2 respectively.
However, the cumulative gain of the 2x leveraged product over the 2 day period (i.e. 20.96%) is greater than two times of the cumulative gain (i.e. 20.48%) of the underlying index over the same period.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 4 % 8 % - - Day 2 6 % 12 % 10.24% = [(1+4%) x (1+6%)] -1 20.96% = [(1+8%) x (1+12%)] – 1 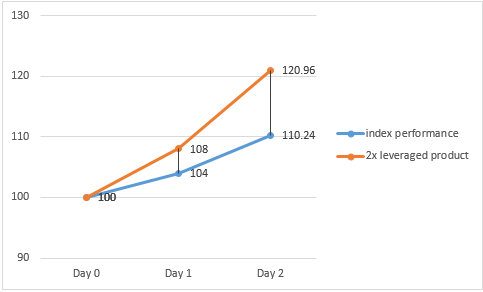
- Downwards trending market
In a downwards trending market where the underlying index drops by 4% and 6% on Day 1 and Day 2 respectively, the 2x leveraged product will make a loss of 8% and 12% on Day 1 and Day 2 respectively.
However, the cumulative loss of the 2x leveraged product over the 2 day period (i.e. -19.04%) is less than two times of the cumulative loss (i.e. -19.52%) of the underlying index over the same period.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -4 % -8 % - - Day 2 -6 % -12 % -9.76% = [(1-4%) x (1-6%)] -1 -19.04% = [(1-8%) x (1-12%)] – 1 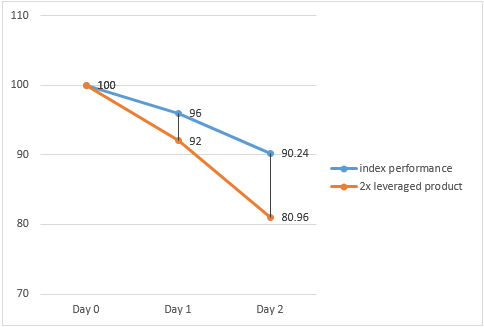
- Volatile market 1
In a volatile market where the underlying index rises by 5% on Day 1 but drops by 4.76% on Day 2, the 2x leveraged product will make a gain of 10% on Day 1 and a loss of 9.52% on Day 2 respectively.
However, at the end of Day 2, the 2x leveraged product will make a cumulative loss of 0.47%, while the underlying index level remain the same as that at the start of Day 1.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 5 % 10 % - - Day 2 -4.76 % -9.52 % 0% = [(1+5%) x (1-4.76%)] -1 -0.47% = [(1+10%) x (1-9.52%)] – 1 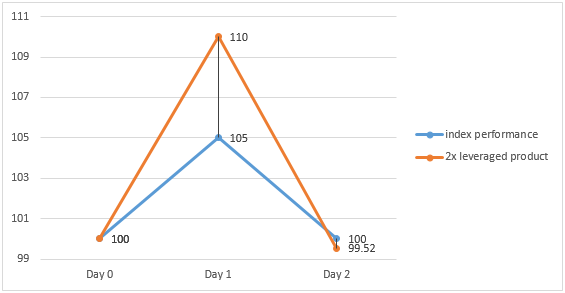
As illustrated in the example for volatile market, it is possible that investors holding 2x leveraged products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up flat.
- Volatile market 2
In a volatile market where the underlying index drops by 30% and 20% on Day 1 and Day 2 respectively, and rises by 90% on Day 3, the 2x leveraged product will make a loss of 60% and 40% on Day 1 and Day 2 respectively and make a gain of 180% on Day 3.
However, at the end of Day 3, the 2x leveraged product will make a cumulative loss of 32.8%, while the underlying index will make a cumulative gain of 6.4%.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -30 % -60 % - - Day 2 -20 % -40 % -44% -76% Day 3 90 % 180 % 6.4% = [(1-30%) x (1-20%)x (1+90%)] -1 -32.8% = [(1-60%) x (1-40%)x (1+180%)] – 1 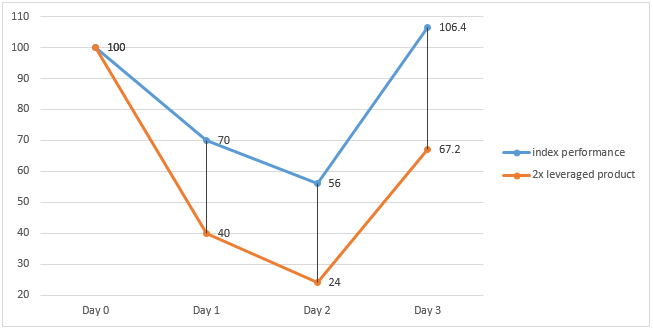
As illustrated in the example for volatile market, it is possible that investors holding 2x leveraged products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up higher.
Holding a 2x leveraged product for longer than one day
- Upwards trending market
In an upwards trending market where the underlying index rises 4% and 6% on Day 1 and Day 2 respectively, the -1x inverse product will make a loss of 4% and 6% on Day 1 and Day 2 respectively.
However, the -1x inverse product’s cumulative loss over the 2 day period (i.e. -9.76%) is less than the opposite of the cumulative gain (i.e. 10.24%) of the underlying index at the end of Day 2.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 4 % -4 % - - Day 2 6 % -6 % 10.24% = [(1+4%) x (1+6%)] -1 -9.76% = [(1-4%) x (1-6%)] – 1 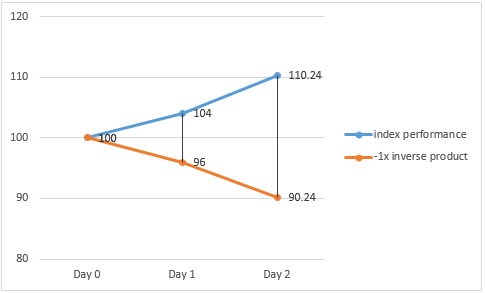
- Downwards trending market
In a downwards trending market where the underlying index drops by 4% and 6% on Day 1 and Day 2 respectively, the -1x inverse product will make a gain of 4% and 6% on Day 1 and Day 2 respectively.
However, the -1x inverse product’s cumulative gain over the 2 day period (i.e. 10.24%) is greater than the opposite of the cumulative loss (i.e. -9.76%) of the underlying index at the end of Day 2.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -4 % 4 % - - Day 2 -6 % 6 % -9.76% = [(1-4%) x (1-6%)] -1 10.24% = [(1+4%) x (1+6%)] – 1 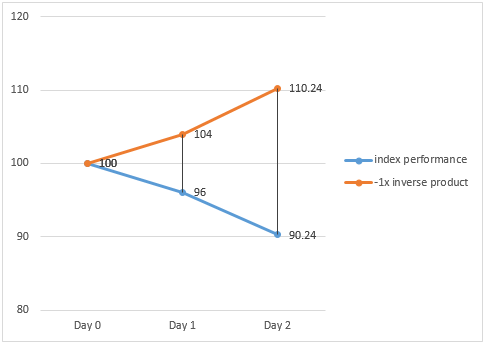
- Volatile market 1
In a volatile market where the underlying index rises by 5% on Day 1 but drops by 4.76% on Day 2, the -1x inverse product will make the loss of the same magnitude as the rise of the underlying index on Day 1 and a gain of the same magnitude as the drop of the underlying index on Day 2.
However, at the end of Day 2, the -1x inverse product will make a cumulative loss of 0.48%, while the underlying index level remain the same as that at the start of Day 1.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 5 % -5 % - - Day 2 -4.76 % 4.76 % 0% = [(1+5%) x (1-4.76%)] -1 -0.48% = [(1-5%) x (1+4.76%)] – 1 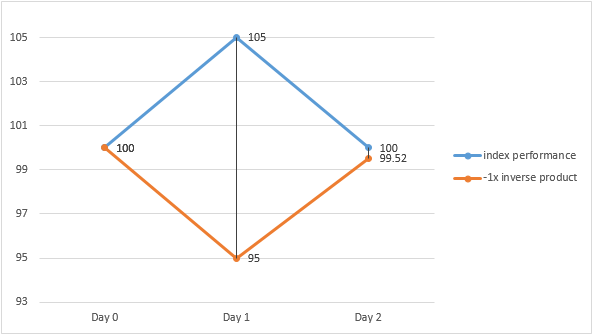
As illustrated in the example for volatile market, it is possible that investors holding -1x inverse products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up flat.
- Volatile market 2
In a volatile market where the underlying index drops by 30% and 20% on Day 1 and Day 2 respectively, and rises by 38% on Day 3, the -1x inverse product will make a gain of 30% and 20% on Day 1 and Day 2 respectively and make a loss of 38% on Day 3.
However, at the end of Day 3, both the -1x inverse product and the underlying index make a cumulative loss.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -30 % 30 % - - Day 2 -20 % 20 % -44% 56% Day 3 38 % -38 % -22.72% = [(1-30%) x (1-20%)x (1+38%)] -1 -3.28% = [(1+30%) x (1+20%)x (1-38%)] – 1 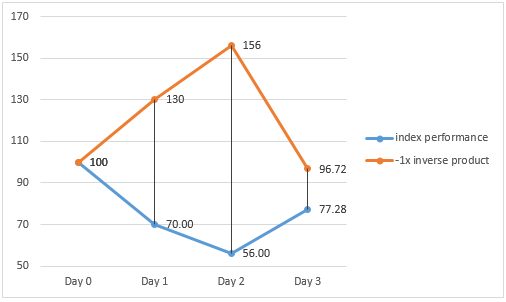
As illustrated in the example for volatile market, it is possible that investors holding -1x inverse products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up lower.
Holding a -1x inverse product for longer than one day
- Upwards trending market
In an upwards trending market where the underlying index rises 4% and 6% on Day 1 and Day 2 respectively, the -2x inverse product will make a loss of 8% and 12% on Day 1 and Day 2 respectively.
However, the -2x inverse product’s cumulative loss over the 2 day period (i.e. -19.04%) is less than the opposite of two times of the underlying index’s cumulative gain (i.e. 20.48%) at the end of Day 2.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 4 % -8 % - - Day 2 6 % -12 % 10.24% = [(1+4%) x (1+6%)] -1 -19.04% = [(1-8%) x (1-12%)] – 1 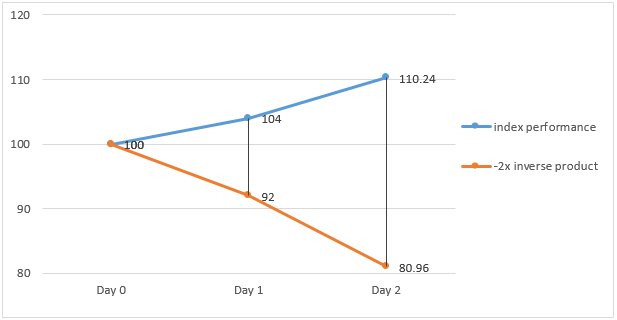
- Downwards trending market
In a downwards trending market where the underlying index drops by 4% and 6% on Day 1 and Day 2 respectively, the -2x inverse product will make a gain of 8% and 12% on Day 1 and Day 2 respectively.
However, the -2x inverse product’s cumulative gain over the 2 day period (i.e. 20.96%) is greater than the opposite of two times of the underlying index’s cumulative loss (i.e. -19.52%) at the end of Day 2.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -4 % 8 % - - Day 2 -6 % 12 % -9.76% = [(1-4%) x (1-6%)] -1 20.96% = [(1+8%) x (1+12%)] – 1 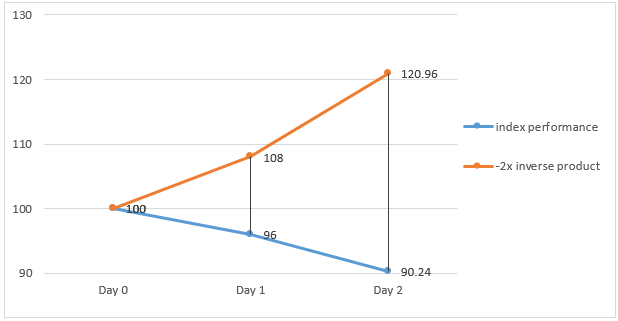
- Volatile market 1
In a volatile market where the underlying index rises by 5% on Day 1 but drops by 4.76% on Day 2, the -2x inverse product will make a loss of 10% on Day 1 and a gain of 9.52% on Day 2 respectively.
However, at the end of Day 2, the -2x inverse product will make a cumulative loss of 1.44%, while the underlying index level remain the same as that at the start of Day 1.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 5 % -10 % - - Day 2 -4.76 % 9.52 % 0% = [(1+5%) x (1-4.76%)] -1 -1.44% = [(1-10%) x (1+9.52%)] – 1 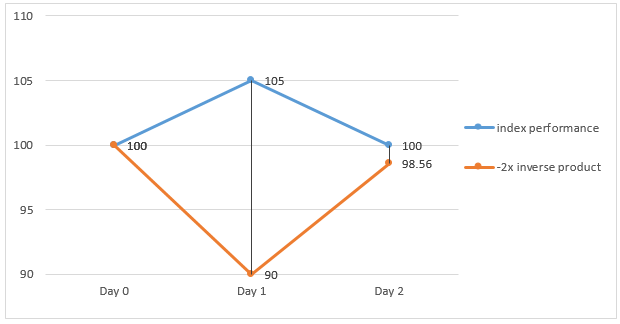
As illustrated in the example for volatile market, it is possible that investors holding -2x inverse products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up flat.
- Volatile market 2
In a volatile market where the underlying index drops by 30% and 20% on Day 1 and Day 2 respectively, and rises by 30% on Day 3, the -2x inverse product will make a gain of 60% and 40% on Day 1 and Day 2 respectively and make a loss of 60% on Day 3.
However, at the end of Day 3, both the -2x inverse product and the underlying index make a cumulative loss.
Index return (Daily) Product return (Daily) Index return (Cumulative) Product return (Cumulative) Day 1 -30 % 60 % - - Day 2 -20 % 40 % -44% 124% Day 3 30 % -60 % -27.2% = [(1-30%) x (1-20%) x (1+30%)] -1 -10.4% = [(1+60%) x (1+40%) x (1-60%) ] – 1 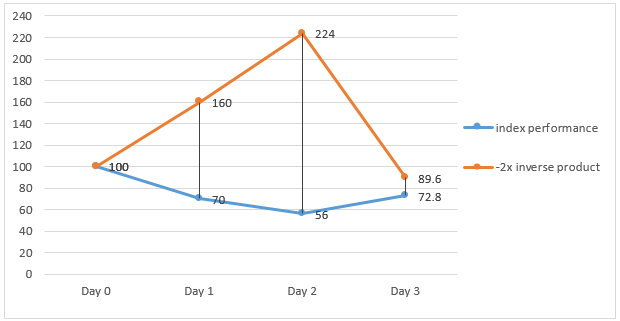
As illustrated in the example for volatile market, it is possible that investors holding -2x inverse products for longer than one day may suffer a loss in a volatile market even if the underlying index ends up lower.
Holding a -2x inverse product for longer than one day
8 May 2019



